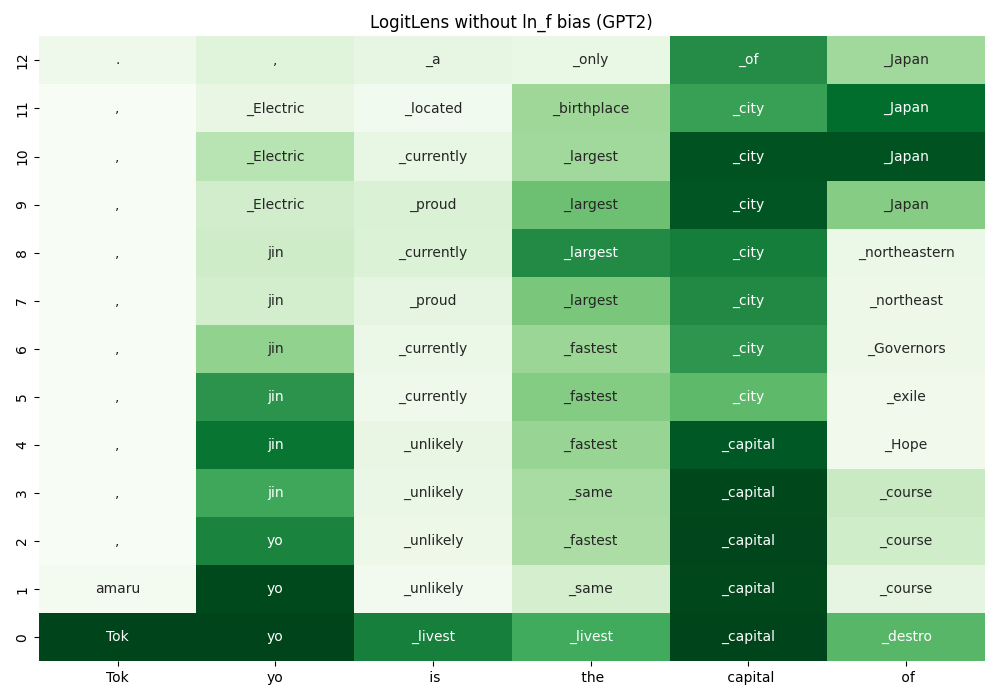
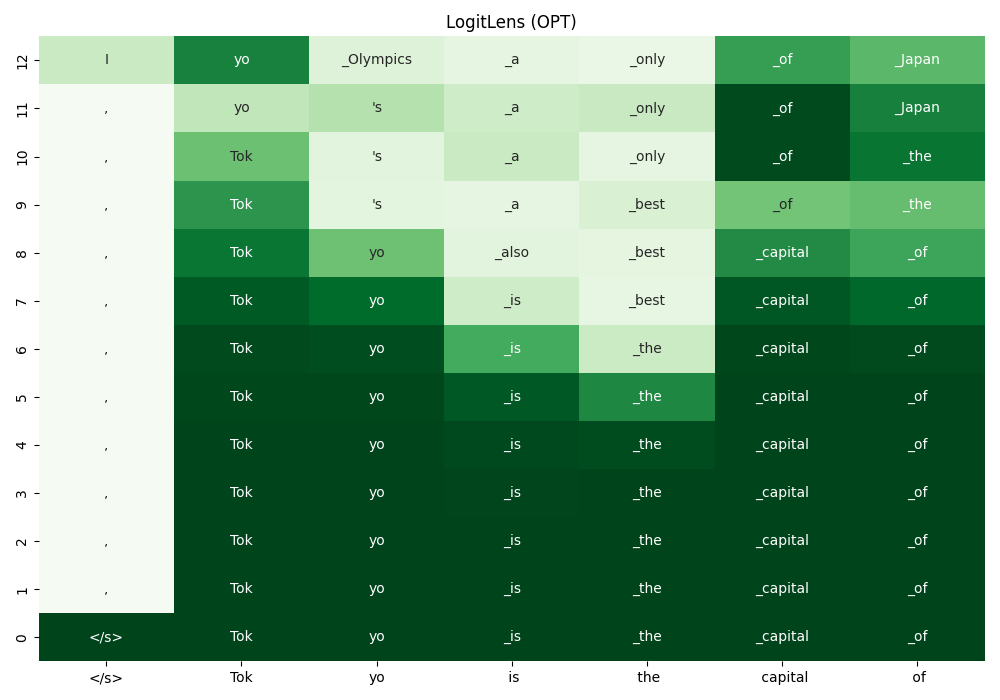
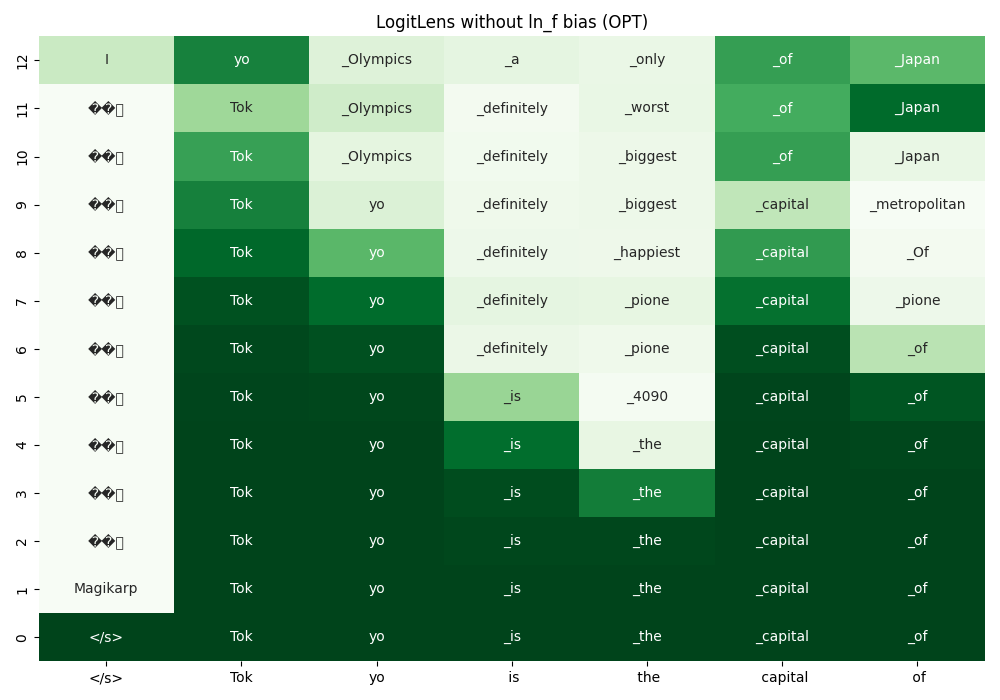
LogitLens[1] applies $\text{LMHead}$ to the internal representations $(\bm{h} \in \mathbb{R}^{1\times d})$ of a transformer model.
\[\begin{equation} \text{LMHead}(\bm{h}) = \text{LN}_\text{f}(\bm{h})\bm{E}^O \label{eq:lm_head} \end{equation}\]Here, $\bm{E}^O \in \mathbb{R}^{d\times |\mathcal{V}|}$ is the unembedding matrix and $\text{LN}_\text{f}$ is the final layer normalization of a transformer model. In this page, we assume LayerNorm (not RMSNorm) is used for $\text{LN}_\text{f}$ , which is defined as follows.
\[\begin{equation} \text{LN}_\text{f}(\bm{h}) = \frac{\bm{x} - \mu(\bm{x})\bm{1}}{\sqrt{\text{Var}(\bm{x})+\varepsilon}}\odot \bm{\gamma} +\bm{\beta} \label{eq:lm_f} \end{equation}\]Here, $\mu(\bm{h}): \mathbb{R}^{d}\rightarrow \mathbb{R}$ is a function that returns element-wise mean of a row-vector $\bm{h}$ and $\bm{\gamma}, \bm{\beta} \in \mathbb{R}^{d}$ are learnable parameters. $\odot$ represents element-wise multiplication.
With LogitLens, one can project the hidden states after each transformer layers to the vocabulary space.
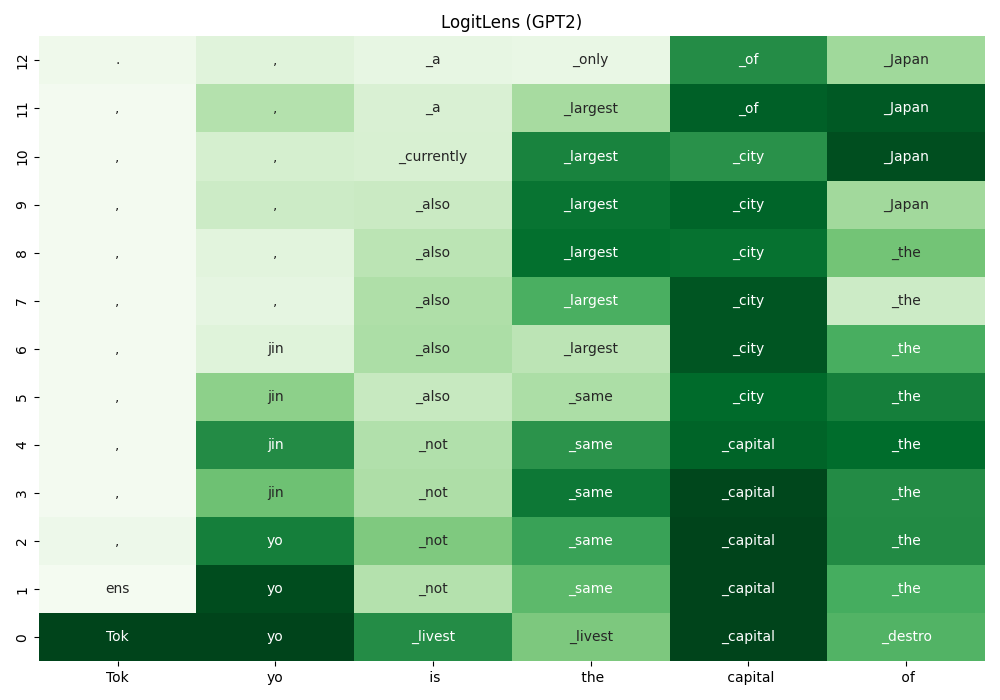
By combining Equation\eqref{eq:lm_head} and \eqref{eq:lm_f}, we get a bias term for the projection to vocabulary space.
\[\begin{align} \text{LogitLens}(\bm{h}) &= \left(\frac{\bm{h} - \mu(\bm{h})\bm{1}}{\sqrt{\text{Var}(\bm{x})+\varepsilon}}\odot \bm{\gamma} + \bm{\beta}\right)\bm{E}^O\\ &= \left(\frac{\bm{h} - \mu(\bm{h})\bm{1}}{\sqrt{\text{Var}(\bm{x})+\varepsilon}}\odot \bm{\gamma}\right)\bm{E}^O + \bm{\beta}\bm{E}^O \label{eq:lm_head_bias} \end{align}\]The second term in Equation\eqref{eq:lm_head_bias}, which is $\bm{\beta}\bm{E}^O \in \mathbb{R}^{|\mathcal{V}|}$ is the bias term, which is added to the result of LogitLens regardless of the input. Adding such bias may not reasonable when analyzing “what the model’s intermediate states represent” as Kobayashi et al. (2023) reports that word frequency in the training corpus is encoded in this bias term of $\text{LN}_\text{f}$ in GPT-2 model.
By removing the bias term, we get the following result.