Attention Bias and Positional Encoding (GPT2)

Attention Decomposition

For sequence with \(n\) tokens \[ \begin{equation} \bm{X} := \begin{bmatrix} \bm{x}_1\\ \vdots\\ \bm{x}_n \end{bmatrix} \hspace{1em} \in \mathbb{R}^{n\times d} \end{equation} \] and weights/biases of \(H\)-head attention \[ \begin{equation} \bm{W}^O := \begin{bmatrix} \bm{W}^O_1\\ \vdots\\ \bm{W}^O_H\\ \end{bmatrix} \hspace{1em} \in \mathbb{R}^{d \times d} \end{equation} \] \[ \begin{align} \bm{W}^Q &:= \begin{bmatrix} \bm{W}^Q_1 & \cdots & \bm{W}^Q_H \end{bmatrix}& \hspace{1em}&\in \mathbb{R}^{d \times d} \label{eq:wq_split}\\ \bm{W}^K &:= \begin{bmatrix} \bm{W}^K_1 & \cdots & \bm{W}^K_H \end{bmatrix}& \hspace{1em}&\in \mathbb{R}^{d \times d} \label{eq:wk_split}\\ \bm{W}^V &:= \begin{bmatrix} \bm{W}^V_1 & \cdots & \bm{W}^V_H \end{bmatrix}& \hspace{1em}&\in \mathbb{R}^{d \times d}\label{eq:wv_split}\\ \bm{b}^Q &:= \begin{bmatrix} \bm{b}^Q_1 & \cdots & \bm{b}^Q_H \end{bmatrix}& \hspace{1em}&\in \mathbb{R}^{d} \label{eq:bq_split}\\ \bm{b}^K &:= \begin{bmatrix} \bm{b}^K_1 & \cdots & \bm{b}^K_H \end{bmatrix}& \hspace{1em}&\in \mathbb{R}^{d} \label{eq:bk_split}\\ \bm{b}^V &:= \begin{bmatrix} \bm{b}^V_1 & \cdots & \bm{b}^V_H \end{bmatrix}& \hspace{1em}&\in \mathbb{R}^{d} \label{eq:bv_split} \end{align} \] where \(\bm{W}^O_i \in \mathbb{R}^{d'\times d}\), \(\bm{W}^Q_i, \bm{W}^K_i, \bm{W}^V_i \in \mathbb{R}^{d\times d'}\), \(\bm{b}^Q_i, \bm{b}^K_i, \bm{b}^V_i \in \mathbb{R}^{d'}\) denoting dimention of hidden-state by \(d\) and dimention of each head by \(d'\), and \(\bm{b^O}\in\mathbb{R}^d\), using \[ \begin{alignat}{4} &\alpha_{i, j, h} &:=& \underset{\bm{x}_j\in \bm{X}}{\text{softmax}^*}\left(\frac{q_h(\bm{x}_i)k_h(\bm{x}_j)^\top}{\sqrt{d'}}\right) &\hspace{0.5em}\in& \mathbb{R}\label{eq:mhsa_alpha}\\ &q_h(\bm{x}) & :=& \bm{x}\bm{W}^Q_h+\bm{b}^Q_h &\hspace{0.5em}\in& \mathbb{R}^{d'}\\ &k_h(\bm{x}) & :=& \bm{x}\bm{W}^K_h+\bm{b}^K_h &\hspace{0.5em}\in& \mathbb{R}^{d'}\\ &v_h(\bm{x}) & :=& \bm{x}\bm{W}^V_h+\bm{b}^V_h &\hspace{0.5em}\in& \mathbb{R}^{d'}\\ \end{alignat} \] attention computation can be expressed as follows. \[ \begin{align} &\text{ATTN}(\bm{x}_i, \bm{X})\nonumber\\ &=\left[\text{head}_1(\bm{x}_i, \bm{X})\hspace{0.5em}\cdots\hspace{0.5em}\text{head}_H(\bm{x}_i, \bm{X})\right] % \begin{bmatrix} % \text{head}_1(\bm{x}_i, \bm{X})&\cdots&\text{head}_H(\bm{x}_i, \bm{X}) % \end{bmatrix} \bm{W}^O + \bm{b}^O\\ &=\sum_{h=1}^H \text{head}_h(\bm{x}_i, \bm{X})\bm{W}^O_h + \bm{b}^O\\ &=\sum_{h=1}^H \left(\sum_{j=1}^n \alpha_{i, j, h} v_h(\bm{x}_i)\right)\bm{W}^O_h + \bm{b}^O\\ &=\sum_{h=1}^H \left(\sum_{j=1}^n \alpha_{i, j, h} \bm{x}_i\bm{W}^V_h + \bm{b}^V_h\right)\bm{W}^O_h + \bm{b}^O\\ &= \sum_{h=1}^H \sum_{j=1}^n \alpha_{i, j, h} \bm{x}_i\bm{W}^V_h\bm{W}^O_h + \bm{b}^V\bm{W}^O + \bm{b}^O\\ &= \sum_{h=1}^H \sum_{j=1}^n \alpha_{i, j, h} \bm{x}_i\bm{W}^{VO}_h + \bm{b}^{VO} \end{align} \]

Regarding Eq.\ref{eq:mhsa_alpha}, \(\text{softmax}^*\) represents softmax with causal mask and \begin{align} &q_h(\bm{x}_i)k_h(\bm{x}_j)^\top\\ &=(\bm{x_i}\bm{W_h^Q}+\bm{b}_h^Q)(\bm{x_j}\bm{W}^K_h+\bm{b}^K_h)^\top\\ &=(\bm{x_i}\bm{W_h^Q}+\bm{b}_h^Q)(\bm{W}^K_h{}^\top\bm{x_j}^\top+\bm{b}^K_h{}^\top)\\ &=(\bm{x_i}\bm{W_h^Q}+\bm{b}_h^Q)\bm{W}^K_h{}^\top\bm{x_j}^\top\nonumber\\ &\phantom{=}+(\bm{x_i}\bm{W_h^Q}+\bm{b}_h^Q)\bm{b}^K_h{}^\top\label{eq:mhsa_score_decomp} \end{align} Now, adding constant value to the input of softmax does not change the result of softmax: \[ \begin{align} &\text{softmax}( \begin{bmatrix} x_1 & \cdots & x_s \end{bmatrix} )\\ &= \frac{1}{\sum_{j=1}^s e^{x_j}} \begin{bmatrix} e^{x_1} & \cdots & e^{x_s} \end{bmatrix} \\ &= \frac{e^c}{e^c \sum_{j=1}^s e^{x_j}} \begin{bmatrix} e^{x_1} & \cdots & e^{x_s} \end{bmatrix} \\ &= \frac{1}{\sum_{j=1}^s e^{x_j+c}} \begin{bmatrix} e^{x_1+c} & \cdots & e^{x_s+c} \end{bmatrix} \\ &=\text{softmax}( \begin{bmatrix} x_1+c & \cdots & x_s+c \end{bmatrix} ) \end{align} \] Therefore, when computing \(\underset{\bm{x}_j\in \bm{X}}{\text{softmax}^*}\), second term in Eq.\ref{eq:mhsa_score_decomp} is a constant and have no effect on \(\alpha_{i,j,h}\). By ignoring the term, \[ \begin{align} &q_h(\bm{x}_i)k_h(\bm{x}_j)^\top\\ &\rightarrow(\bm{x_i}\bm{W_h^Q}+\bm{b}_h^Q)\bm{W}^K_h{}^\top\bm{x_j}^\top\\ &=\bm{x_i}\bm{W_h^Q}\bm{W}^K_h{}^\top\bm{x_j}^\top + \bm{b}_h^Q\bm{W}^K_h{}^\top\bm{x_j}^\top\label{eq:mhsa_score_decomp_2} \end{align} \] The first term can be interpreted as the similarity between key vector and query vector. The second term can be interpreted as the (semi-)bias term deriving from the key token regardless of the query token.

Positional Encoding

GPT2 models use learned positional encoding \(\bm{P} \in \mathbb{R}^{l\times d}\). The learned weight is:

Although not much can be interpreted from the figure itself, a new point of view can be gained by computing \(\bm{b}_h^Q\bm{W}^K_h{}^\top\bm{P}^\top\), the second term in Eq.\ref{eq:mhsa_score_decomp_2}, at the first transformer layer.

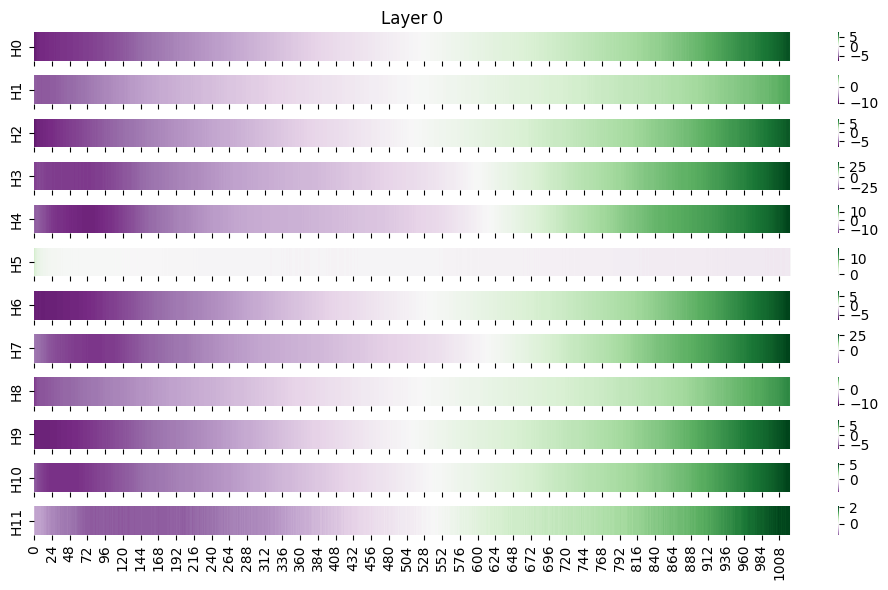
The purple scores represent negative score, and the green scores represent positive score. Considering that GPT2 is a causal model attending only to the past tokens, the figure shows larger attention weights put to close tokens, and smaller attention weights put to distant tokens. This supports "detokenization" hypothesis, "which suggests that the model concatenates nearby tokens that are part of the same underlying word or entity." ( Lad et. al. 2023 )

Regarding the token embeddings, the following shows the relation between the norm of token embeddings and the (semi-)bias term of attention weights at the first transformer layer.

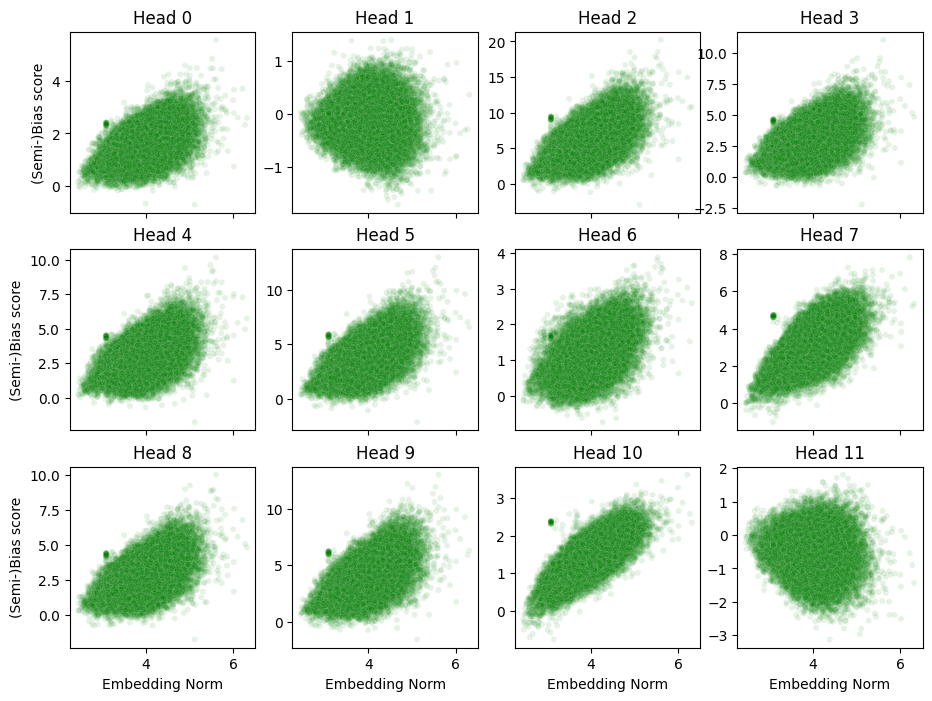
The result shows positive correlation at most attention heads, especially at Head-7 and Head-10.