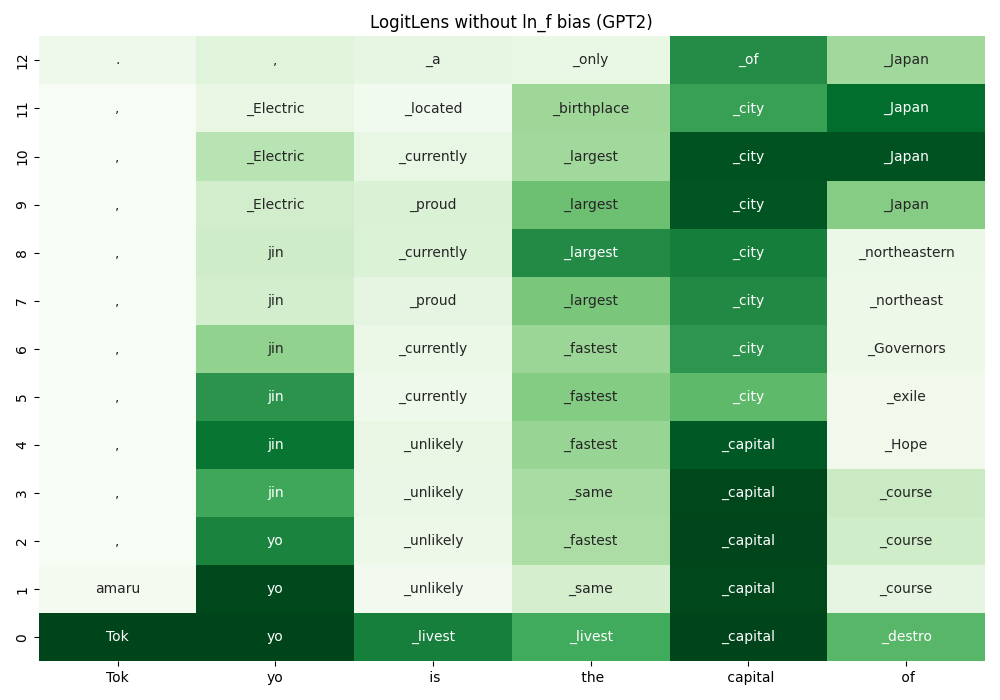
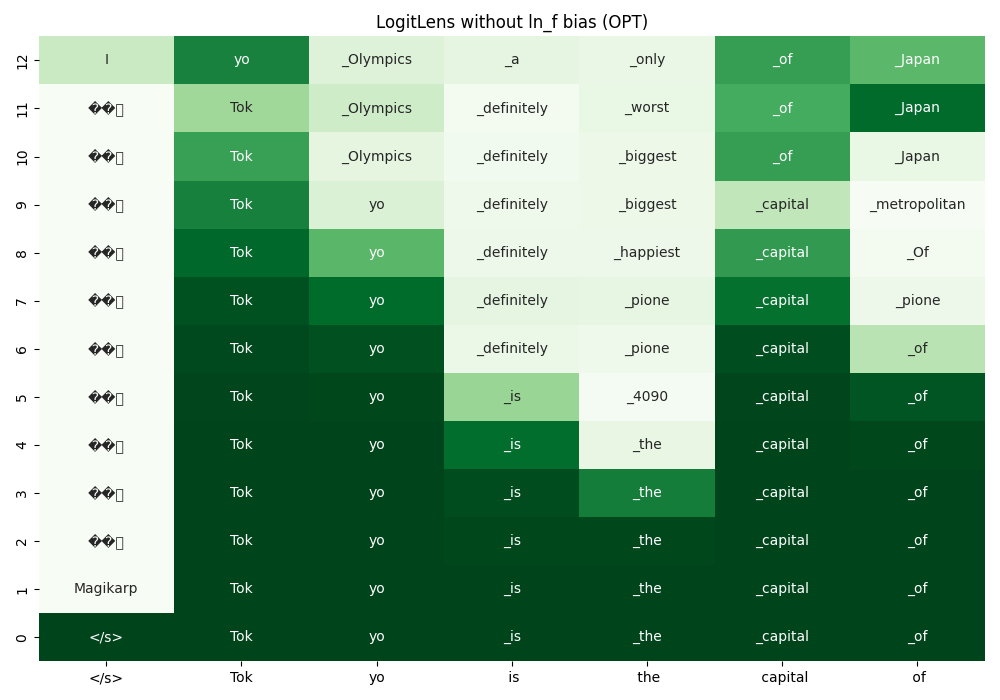
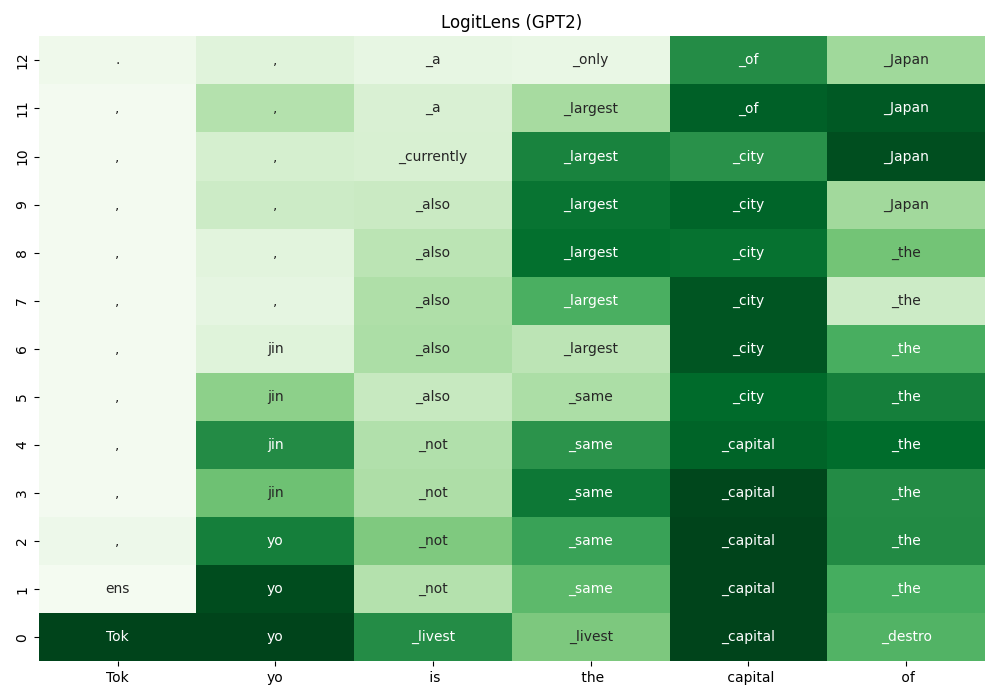
LogitLens without bias (GPT2)

LogitLens applies \(\text{lm_head}\) to the hidden states \((\bm{h} \in \mathbb{R}^{1\times d})\) of the transformer model.
\[ \begin{equation} \text{lm_head}(\bm{h}) = \text{ln_f}(\bm{h})\bm{W} \label{eq:lm_head} \end{equation} \] \[ \begin{equation} \text{ln_f}(\bm{h}) = \frac{\bm{h} - \mu(\bm{h})\bm{1}}{s(\bm{h})}\odot \bm{\gamma} + \bm{\beta} \label{eq:lm_f} \end{equation} \] Here, \(\bm{W} \in \mathbb{R}^{d\times v}\) is the unembedding matrix, \(\mu(\bm{h})\) and \(s(\bm{h})\) is the element-wise mean and the standard deviation of \(\bm{h}\), respectively, \(\bm{\gamma}, \bm{\beta} \in \mathbb{R}^{1\times d}\) are learnable parameters, and \(\odot\) represents element-wise multiplication.

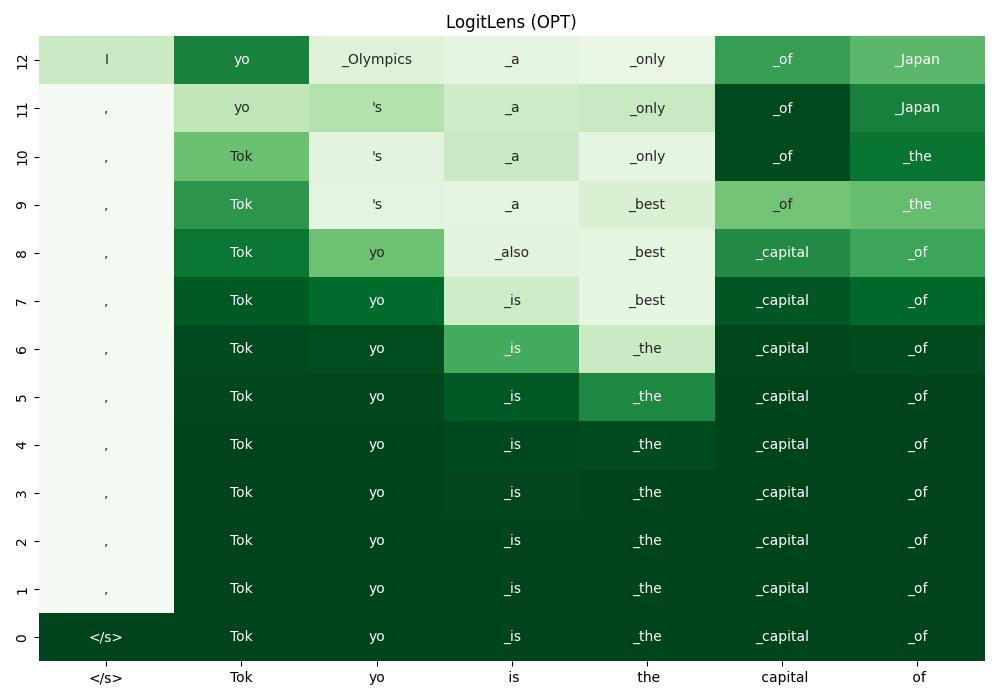
With LogitLens, one can project the hidden states after each transformer layers to the vocabulary space.

Example of LogitLens.

By combining Equation\eqref{eq:lm_head} and \eqref{eq:lm_f}, we get a bias term for the projection to vocabulary space. \[ \begin{align} \text{LogitLens}(\bm{h}) &= \left(\frac{\bm{h} - \mu(\bm{h})\bm{1}}{s(\bm{h})}\odot \bm{\gamma} + \bm{\beta}\right)\bm{W}\\ &= \left(\frac{\bm{h} - \mu(\bm{h})\bm{1}}{s(\bm{h})}\odot \bm{\gamma}\right)\bm{W} + \bm{\beta}\bm{W} \label{eq:lm_head_bias} \end{align} \]

The second term in Equation\eqref{eq:lm_head_bias} is the bias term, which is added to the result of LogitLens regardless of the input.
Adding such bias is not reasonable when analyzing "what the model's intermediate states represent".
(In GPT2, Kobayashi et al. (2023) reports that word frequency in the training corpus is encoded in this bias.)
By removing the bias term, we get the following result.